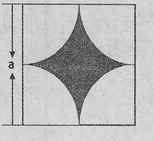
如图所示，墙上挂有边长为a的正方形木板，它的四个角的空白部分-优题课

游客

题文

如图所示，墙上挂有边长为a的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为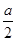的圆弧，某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则它击中阴影部分的概率是（）

A．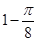

B．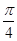

C．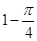

D．与a的值有关联

科目数学题型选择题难度中等

登录免费查看答案和解析

相关试题

集合 $M = \{x | l g x > 0\}$ ， $N = \{x | x^{2} \leq 4\}$ ，则 $M \cap N =$ （）

A．

(1, 2)

B．

[1, 2)

C．

(1, 2]

D．

[1, 2]

设函数 $f (x) = 2 x - \cos x$ ， $\{a_{n}\}$ 是公差为 $\frac{π}{8}$ 的等差数列， $f (a_{1}) + f (a_{2}) + \dots + f (a_{5}) = 5 π$ ，则 ${[f (a_{3})]}^{2} - a_{1} a_{3} =$ （）

A．

0

B．

\frac{1}{16} π^{2}

C．

\frac{1}{8} π^{2}

D．

\frac{13}{16} π^{2}

方程 $a y = b^{2} x^{2} + c$ 中的 $a, b, c \in \{- 3, - 2, 0, 1, 2, 3\}$ ,且 $a, b, c$ 互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有（）

如图，半径为 $R$ 的半球 $O$ 的底面圆 $O$ 在平面 $α$ 内，过点 $O$ 作平面 $α$ 的垂线交半球面于点 $A$ ，过圆 $O$ 的直径 $C D$ 作平面 $α$ 成 $45 °$ 角的平面与半球面相交，所得交线上到平面 $α$ 的距离最大的点为 $B$ ，该交线上的一点 $P$ 满足 $∠ B O P = 60 °$ ，则 $A$ 、 $P$ 两点间的球面距离为（）

A．

R a r c \cos \frac{\sqrt{2}}{4}

B．

\frac{π R}{4}

C．

R a r c \cos \frac{\sqrt{3}}{3}

D．

\frac{π R}{3}

某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗 $A$ 原料1千克、 $B$ 原料2千克；生产乙产品1桶需耗 $A$ 原料2千克， $B$ 原料1千克.每桶甲产品的利润是300元，每桶乙产品的利润是400元.公司在生产这两种产品的计划中，要求每天消耗 $A$ 、 $B$ 原料都不超过12千克.通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（）