（本小题满分14分）
某单位为解决职工的住房问题，计划征用一块土地盖一幢总建筑面积为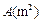
的宿舍楼．已知土地的征用费为2388元/
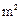，且每层的建筑面积相同，土地的征用面积为第一层的2．5倍．经工程技术人员核算，第一．二层的建筑费用都为445元/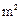，以后每增高一层，其建筑费用就增加30元/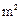．试设
计这幢宿舍楼的楼高层数，使总费用最小，并求出其最小费用．（总费用为建筑费用和征地费用之和）
某医院一天派出医生下乡医疗，派出医生人数及其概率如下：
| 医生人数 |
0 |
1 |
2 |
3 |
4 |
5人及以上 |
| 概率 |
0.1 |
0.16 |
x |
y |
0.2 |
z |
(1)若派出医生不超过2人的概率为0.56，求x的值；
(2)若派出医生最多4人的概率为0.96，最少3人的概率为0.44，求y、z的值．
已知关于x的一元二次方程x2－2(a－2)x－b2＋16＝0.
(1)若a、b是一枚骰子掷两次所得到的点数，求方程有两正根的概率；
(2)若a∈[2，4]，b∈[0，6]，求方程没有实根的概率．
设函数f(x)＝x2＋bx＋c，其中b、c是某范围内的随机数，分别在下列条件下，求事件A“f(1)≤5且f(0)≤3”发生的概率．
(1)若随机数b，c∈{1，2，3，4}；
(2)已知随机函数Rand()产生的随机数的范围为{x|0≤x≤1}，b，c是算法语句b＝4*Rand()和c＝4*Rand()的执行结果．(注：符号“*”表示“乘号”)
如图，∠AOB＝60°，OA＝2，OB＝5，在线段OB上任取一点C，试求：
(1)△AOC为钝角三角形的概率；
(2)△AOC为锐角三角形的概率．
下表中有三个游戏规则，袋子中分别装有大小相同的球，从袋子中取球，分别计算甲获胜的概率，说明哪个游戏是公平的？
| 游戏1 |
游戏2 |
游戏3 |
| 1个红球和1个白球 |
2个红球和2个白球 |
3个红球和1个白球 |
| 取1个球 |
取1个球，再取1个球 |
取1个球，再取1个球 |
| 取出的球是红球→甲胜 |
取出的两个球同色→甲胜 |
取出的两个球同色→甲胜 |
| 取出的球是白球→乙胜 |
取出的两个球不同色→乙胜 |
取出的两个球不同色→乙胜 |