如图放置的边长为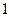 的正三角形
的正三角形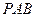 沿
沿 轴滚动,设顶点
轴滚动,设顶点 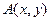 的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是 ,则
,则 在区间
在区间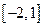 上的解析式是 ;(说明:“正三角形
上的解析式是 ;(说明:“正三角形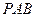 沿x轴滚动”包括沿x轴正方向和
沿x轴滚动”包括沿x轴正方向和 沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形
沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形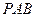 也可以沿x轴负方向逆时针滚动)
也可以沿x轴负方向逆时针滚动)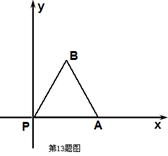
圆O有一内接正三角形,向圆O内随机投一点,则该点落在内接正三角形内的概率是 .
把一颗骰子抛掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,组成方程组 则(1)在出现点数有2的情况下,方程组只有一个解的概率为 .
则(1)在出现点数有2的情况下,方程组只有一个解的概率为 .
(2)只有正数解的概率为 .
某人有甲、乙两个电子密码箱,欲存放A,B,C三份不同的重要文件,则两个密码箱都不空的概率是 .
一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是 .
在集合A={2,3}中随机取一个元素m,在集合B={1,2,3}中随机取一个元素n,得到点P(m,n),则点P在圆x2+y2=9内部的概率为 .