（本小题满分12分）
甲乙两个学校高三年级分别为1100人，1000人，为了统计两个学校在地区二模考试的数学科目成绩，采用分层抽样抽取了105名学生的成绩，并作出了部分频率分布表如下：（规定考试成绩在[120，150]内为优秀）
甲校：
| 分组 |
 |
 |
 |
 |
 |
 |
 |
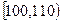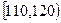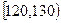[140,150] |
| 频数 |
2 |
3 |
10 |
15 |
15 |
x |
3 |
1 |
乙校：
| 分组 |
|
|
|
|
|
|
|
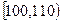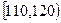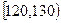[140,150] |
| 频数 |
1 |
2 |
9 |
8 |
10 |
10 |
y |
3 |
（1）计算x，y的值，并分别估计两上学校数学成绩的优秀率；
（2）由以上统计数据填写下面2×2列联表，并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| |
甲校 |
乙校 |
总计 |
| 优秀 |
|
|
|
| 非优秀 |
|
|
|
| 总计 |
|
|
|
附：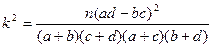
 |
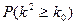0．10 |
0．025 |
0．010 |
 |
2．706 |
5．024 |
6．635 |
已知
．
（1）若曲线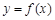
在
处的切线与直线
平行，求a的值；
（2）当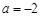
时，求
的单调区间．
如图，椭圆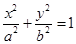
上的点M与椭圆右焦点
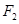的连线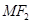
与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．
（1）求椭圆的离心率；
（2）F1是椭圆的左焦点，C是椭圆上的任一点，证明：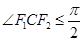
；
（3）过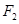且与AB垂直的直线交椭圆于P、Q，若
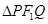的面积是20
，求此时椭圆的方程．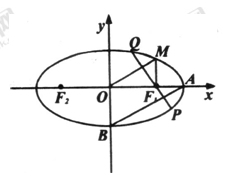
设函数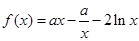
.
（1）若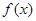
在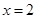
时有极值，求实数
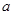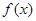的值和的极大值；
（2）若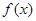在定义域上是增函数,求实数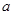的取值范围．
已知椭圆C的两焦点分别为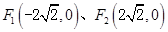
，长轴长为6，
⑴求椭圆C的标准方程;
⑵已知过点（0，2）且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。.
在如图所示的多面体ABCDE中，AB⊥平面ACD,DE⊥平面ACD，AC=AD=CD=DE=2，AB=1。
（1）请在线段CE上找到一点F，使得直线BF∥平面ACD，并证明；
（2）求平面BCE与平面ACD所成锐二面角的大小；