设 ,函数
,函数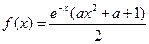 ,其中e是自然对数的底数。
,其中e是自然对数的底数。
(1)求a=-1时,求 在[-1,2]上的最小值;
在[-1,2]上的最小值;
(2)求函数 在R上的单调区间;
在R上的单调区间;
(3)若a为常数,且 是否存在实数t,使得对于任意
是否存在实数t,使得对于任意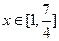 ,
, 恒成立,存在,求出t的范围,不存在,说明理由。
恒成立,存在,求出t的范围,不存在,说明理由。
已知
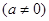 ,
,
(I)判断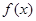 的奇偶性;
的奇偶性;
(II)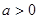 时,判断
时,判断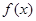 在
在 上的单调性并给出证明。
上的单调性并给出证明。
( 本题满分12分)已知
本题满分12分)已知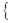
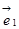 ,
, 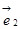
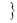 是平面上的一组基底,若
是平面上的一组基底,若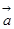
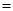
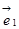 +λ
+λ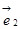 ,
,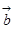
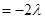
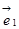
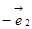 ,
,
(I)若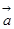 与
与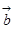 共线,求
共线,求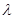 的值;
的值;
(II)若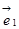 、
、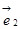 是夹角为
是夹角为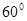 的单位向量,当
的单位向量,当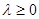 时,求
时,求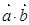 的最大值。
的最大值。
已知向量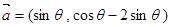 ,
,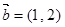 ,
,
(I)若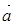 ∥
∥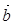 ,求
,求
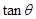 的值;
的值;
(II)若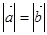 ,
,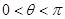 求
求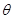 的值。
的值。
已知函数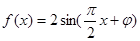 (其中0≤
(其中0≤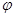 ≤
≤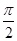 )的图象与y轴交于点
)的图象与y轴交于点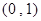 ,
,
(I)求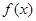 的解析式;
的解析式;
(II)如图,设P是图象上的最高点,M、N是图象与x轴的交点,求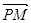 与
与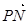 的夹角的余弦值。
的夹角的余弦值。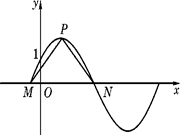
如图,已知椭圆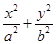 (a>b>0)的离心率
(a>b>0)的离心率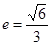 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为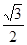 .
.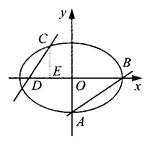
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.