已知函数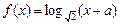 的图象过原点。
的图象过原点。
(1)求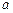 的值;
的值;
(2)若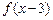 ,
,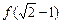 ,
,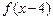 成等差数列,求
成等差数列,求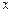 的值。
的值。
(本小题满分10分)
已知函数 。
。
(1)当 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)若对任意 , 恒有
, 恒有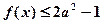 ,求
,求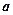 的取值范围。
的取值范围。
(本小题满分10分)椭圆 的离心率为
的离心率为 ,且过点
,且过点 。
。
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 交于两点
交于两点 ,
,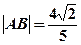 ,求
,求 的值。
的值。
(本小题满分9分)要制做一个体积为72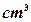 的长方体带盖箱子,并且使长宽之比为
的长方体带盖箱子,并且使长宽之比为 ,设箱子的表面积为
,设箱子的表面积为 ,宽为
,宽为 。
。
(1)写出箱子的表面积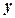 关于宽
关于宽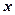 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(2)求箱子的表面积的最小值及取得最小值时的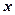 的值。
的值。
(本小题满分9分)命题 :“方程
:“方程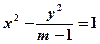 表示焦点在
表示焦点在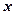 轴上的双曲线”,命题
轴上的双曲线”,命题 :“在区间
:“在区间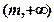 上,函数
上,函数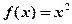 单调递增”,若
单调递增”,若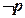 是真命题,
是真命题,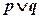 是真命题,求实数
是真命题,求实数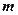 的取值范围。
的取值范围。
(本小题满分12分)设函数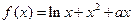 .
.
(Ⅰ)若x=时,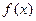 取得极值,求
取得极值,求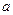 的值;
的值;
(Ⅱ)若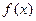 在其定义域内为增函数,求
在其定义域内为增函数,求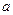 的取值范围。
的取值范围。