如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是线段BC上一点,以AE为边在直线MN的上方作正方形AEFG

连结GD,求证△ADG≌△ABE;
如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=1,BC=2,E是线段BC上一动点(不含端点B,C ),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当E由B向C运动时,∠FCN的大小是否保持不变,若∠FCN的大小不变,求tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
如图,点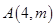 是反比例函数
是反比例函数 (x>0)的图象上一点,
(x>0)的图象上一点,
 轴正半轴于
轴正半轴于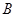 ,
, 是
是 的中点;一次函数
的中点;一次函数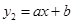 的图象过
的图象过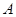 、
、 两点,并交于
两点,并交于 轴于
轴于 .
.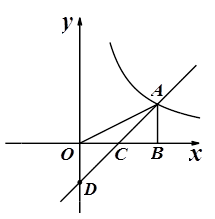
(1)直接写出点 、
、 的坐标;
的坐标;
(2)求一次函数和反比例函数的解析式;
(3)观察图象,请指出在 轴的右侧,当
轴的右侧,当 时
时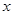 的取值范围.
的取值范围.
甲、乙两辆汽车同时分别从 、
、 两城沿同一条高速公路匀速驶向
两城沿同一条高速公路匀速驶向 城.已知
城.已知 、
、 两城的距离为
两城的距离为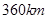 ,
, 、
、 两城的距离为
两城的距离为 ,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为
,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为 km/h.
km/h.
(1)根据题意填写下表:
| 行驶的路程(km) |
速度(km/h) |
所需时间(h) |
|
| 甲车 |
360 |
||
| 乙车 |
320 |
 |
(2)求甲、乙两车的速度.
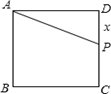
如图,正方形 的边长为
的边长为 ,
,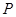 是
是 边上一点.设
边上一点.设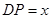 ,四边形
,四边形 的面积为
的面积为 .
.
(1)求 关于
关于 的函数关系式,并写出自变量x的取值范围;
的函数关系式,并写出自变量x的取值范围;
(2)画出(1)中的这个函数图象.
已知 是
是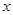 的一次函数,且当
的一次函数,且当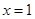 时,
时, ;当
;当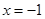 时,
时,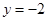 .
.
(1)求这个函数的解析式;
(2)求出这条直线与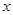 轴的交点坐标.
轴的交点坐标.
先化简,再求值: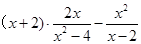 ,其中
,其中 .
.