(本小题满分14分)某地区的农产品 第
第 天
天 的销售价格
的销售价格 (元∕百斤),一农户在第
(元∕百斤),一农户在第 天
天 农产品
农产品 的销售量
的销售量 (百斤)。
(百斤)。
(1)求该农户在第7天销售农产品 的收入;
的收入;
(2)问这20天中该农户在哪一天的销售收入最大?
(本小题满分12分)已知等比数列 的前n项和为
的前n项和为 ,且满足
,且满足 .
.
(I)求p的值及数列 的通项公式;
的通项公式;
(II)若数列 满足
满足 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分12分)在四棱锥 ,
, 平面ABCD,PA=2.
平面ABCD,PA=2.
(I)设平面 平面
平面 ,求证:
,求证: ;
;
(II)设点Q为线段PB上一点,且直线QC与平面PAC所成角的正切值为 ,求
,求 的值.
的值.
(本小题满分12分)为了参加市中学生运动会,某校从四支较强的班级篮球队A,B,C,D中选出12人组成校男子篮球队,队员来源如下表:
(I)从这12名队员中随机选出两名,求两人来自同一个队的概率;
(II)比赛结束后,学校要评选出3名优秀队员(每一个队员等可能被评为优秀队员),设其中来自A队的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)在 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,且
,且 成等差数列.
成等差数列.
(I)若 的值;
的值;
(II)设 ,求t的最大值.
,求t的最大值.
选修4—5:不等式选讲
设不等式 的解集为
的解集为 , 且
, 且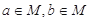 .
.
(Ⅰ) 试比较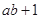 与
与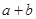 的大小;
的大小;
(Ⅱ) 设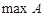 表示数集
表示数集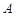 中的最大数, 且
中的最大数, 且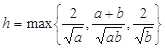 , 求
, 求 的范围.
的范围.