(本小题满分16分)已知在直角坐标系中, ,其中数列
,其中数列 都是递增数列。
都是递增数列。
(1)若 ,判断直线
,判断直线 与
与 是否平行;
是否平行;
(2)若数列 都是正项等差数列,设四边形
都是正项等差数列,设四边形 的面积为
的面积为 .
.
求证: 也是等差数列;
也是等差数列;
(3)若 ,
, ,记直线
,记直线 的斜率为
的斜率为 ,数列
,数列 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列 的个数。
的个数。
已知函数 .
(Ⅰ)在图中画出 的图象;
(Ⅱ)求不等式 的解集.

在直角坐标系 中,曲线C1的参数方程为 (t为参数, ).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线 .
(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(Ⅱ)直线C3的极坐标方程为 ,其中α0满足 ,若曲线C1与C2的公共点都在C3上,求a.
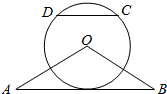
如图,△OAB是等腰三角形, .以O为圆心, 为半径作圆.
(Ⅰ)证明:直线AB与⊙O相切;
(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明: .
已知函数 .
(Ⅰ)讨论 的单调性;
(Ⅱ)若 有两个零点,求a的取值范围.
在直角坐标系xOy中,直线 交y轴于点M,交抛物线 于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(Ⅰ)求 ;
(Ⅱ)除H以外,直线MH与C是否有其它公共点?说明理由.