：如图，四边形ABCD是正方形，PB^平面ABCD，MA∥PB，PB＝AB＝2MA．
（Ⅰ）证明：AC∥平面PMD；
（Ⅱ）求直线BD与平面PCD所成的角的大小；
（Ⅲ）求平面PMD与平面ABCD所成的二面角（锐角）的正切值．
（本小题满分12分）已知函数
的定义域为集合A，函数
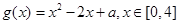的值域为集合B，若
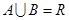， 求实数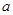
的取值范围．
（本大题满分12分，每小题6分）
（1）计算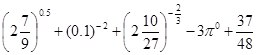
（2）化简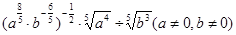
已知函数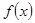
在定义域（0，+∞）上为增函数，且满足
，
．
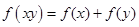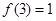（1）求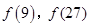
的值；
（2）若
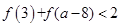，求实数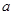
的取值范围．
某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出．当每辆车的月租金每增加50元时，未租出的车将会增加一辆．租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？
(12分)已知函数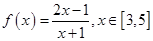
，
（1）用定义法证明函数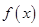
的单调性；
（2）求函数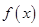的最小值和最大值．