已知：抛物线
经过点
．
（1）求
的值；
（2）若
，求这条抛物线的顶点坐标；
（3）若
，过点
作直线
轴，交
轴于点
，交抛物线于另一点
，且
，求这条抛物线所对应的二次函数关系式．（提示：请画示意图思考）
某养殖户每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为4万元，可变成本逐年增长，已知该养殖户第1年的可变成本为2.6万元，设可变成本平均的每年增长的百分率为x．
（1）用含x的代数式表示第3年的可变成本为万元．
（2）如果该养殖户第3年的养殖成本为7.146万元，求可变成本平均每年增长的百分率x．
用公式法解方程：
．
如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点。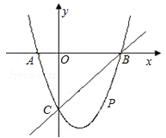
（1）求这个二次函数的表达式。
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由。
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积。
已知二次函数
与x轴的公共点有两个。
求：（1）求k的取值范围；
（2）当k=1时，求抛物线与x轴的公共点A和B的坐标及顶点C的坐标；
（3）观察图象，当x取何值时y＞0?
已知关于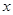
的方程 
.
（1）求证：不论
为任何实数，此方程总有实数根；
（2）若抛物线
与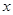轴交于两个不同的整数点，且为正整数，试确定此抛物线的解析式。