(本小题满分12分)
已知等差数列 的前
的前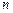 项和为
项和为 ,
,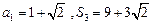
(1)求数列 的通项公式
的通项公式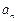 与前
与前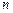 项和
项和 ;
;
(2)设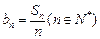 求证:数列
求证:数列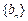 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
(本小题满分12分)
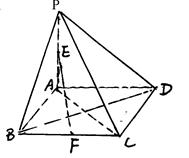
如图,在四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形, 底面
底面 ,
,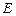 为
为 的中点,
的中点, 为
为 的中点,求证:
的中点,求证:
(1)平面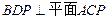 ;
;
(2) .
.
(本小题满分12分)
已知函数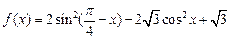
(1)求 最小正周期和单调递减区间;
最小正周期和单调递减区间;
(2)若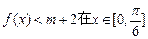 上恒成立,求实数
上恒成立,求实数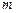 的取值范围。
的取值范围。
((本小题满分12分)已知偶函数 经过点(1,1),
经过点(1,1), 为数列
为数列 的前n项和,点
的前n项和,点 (
( )在曲线
)在曲线 上.
上.
(1)求 的解析式
的解析式
(2)求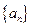 的通项公式
的通项公式
(3)数列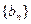 的第n项
的第n项 是数列
是数列 的第
的第 项(
项( ),且
),且 .
.
求和
(本小题满分10分)如果有穷数列 (
(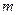 为正整数)满足条件
为正整数)满足条件 ,
,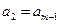 ,…,
,…, ,即
,即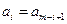 (
(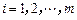 ),我们称其为“对称数列”.
),我们称其为“对称数列”.
例如,数列 与数列
与数列 都是“对称数列”.
都是“对称数列”.
(1)设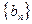 是7项的“对称数列”,其中
是7项的“对称数列”,其中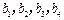 是等差数列,且
是等差数列,且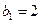 ,
, .依次写出
.依次写出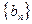 的每一项;
的每一项;
(2)设 是
是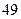 项的“对称数列”,其中
项的“对称数列”,其中 是首项为
是首项为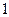 ,公比为
,公比为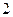 的等比数列,求
的等比数列,求 各项的和
各项的和 ;
;
(3)设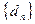 是
是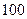 项的“对称数列”,其中
项的“对称数列”,其中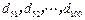 是首项为
是首项为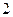 ,公差为
,公差为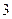 的等差数列.求
的等差数列.求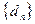 前
前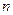 项的和
项的和
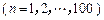 .
.