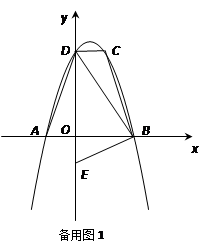
某医药研究所开发了一种新药，在试验药效时发现，假如成人按规定剂量服用，那么服药后2小时时血液中含药量最高，达每毫升6微克，接着逐步衰减，10小时时血液中含药量为每毫升3微克，每毫升血液中含药量y微克随时间x小时的变化如图所示，当成人按规定剂量服药后，
（1）分别求出 x≤2和 x≥2时，y 与x之间的函数关系式
（2）假如每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的，那么这个有效时间是多长？
某商场开展购物抽奖活动，抽奖箱中有3个形状、大小和质地等完全相同的小球，分别标有数字1、2、3．顾客从中随机摸出一个小球，然后放回箱中，再随机摸出一个小球．
(1)利用树形图法或列表法(只选其中一种)，表示摸出小球可能出现的所有结果；
(2)若规定：两次摸出的小球的数字之积为9，则为一等奖；数字之积为偶数，则为二等奖．请你分别求出顾客抽中一等奖、二等奖的概率．
如图，在平面直角坐标系中，已知点
，
轴于A．将点B绕原点逆时针旋转90°后记作点
，作出旋转后的
.
（1）点的坐标为；
（2）求点B所经过的路径长.
已知关于x的方程
.
(1)当方程有两个不相等的实数根时,求k的取值范围;
(2)当方程的一个根是2时,求k的值.
计算：
．
如图，平面直角坐标系中，O为坐标原点，等腰梯形ABCD四个顶点都在抛物线y=ax2+bx+c上，其中点A、B在x轴上，点D在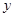
轴上，且CD∥AB, 已知S梯形ABCD=8，tan∠DAO=4，点B的坐标为（2，0），点E坐标为（0，－1）.
（1）求此抛物线的解析式；
（2）若△OEB从点B开始以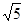
个单位每秒的速度沿BD向终点D匀速运动. 设运动时间为t秒，在整个运动过程中，当边OE与线段AD相交时，求运动时间t的取值范围；
（3）能否将△OEB绕平面内某点旋转90°后使得△OEB的两个顶点落在x轴上方的抛物线上，若能，请直接写出旋转中心的坐标，若不能，请说明理由.
