把数轴画完整,并在在数轴上表示下列各数,然后按从小到大的顺序用“<”号连接.
-3, 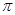 , 2,
, 2, 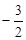 .
.
解方程:① 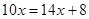 ②
②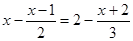
先化简,再求值.
(1)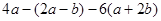 其中
其中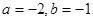 .
.
(2)已知x+3y="3" ,xy=11,求代数式3(x-3y)-(xy+5)+2(3y-2x)的值.
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB.OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A.点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲.乙两种剪法,哪种剪法所得的正方形面积大?请说明理由。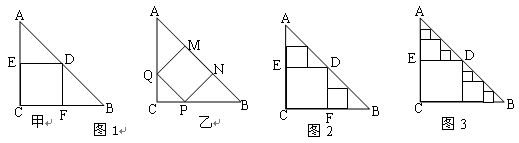
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为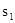 ;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为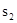 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为
;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为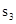 ,继续操作下去……,则第10次剪取时,
,继续操作下去……,则第10次剪取时, ;
;
(3)求第10次剪取后,余下的所有小三角形的面积之和。