如图①,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O。
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图②,P是线段BC上一动点(不与点B、C重合),连接PO并延长交线段AB于点Q,QR⊥BD,垂足为点R。四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积。
(本小题8分)
(1)解方程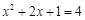 ;
;
(2)利用判别式判断方程 的根的情况.
的根的情况.
如图 将线段
将线段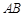 放在每个小正方形的边长为
放在每个小正方形的边长为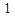 的网格中,点
的网格中,点 ,点
,点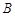 均落在格点上.
均落在格点上.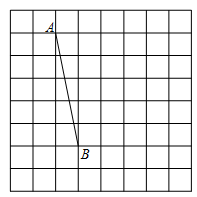
(1)AB的长等于;
(2)请在如图所示的网格中,用无刻度的直尺,在线段AB上画出点P,使 ,并简要说明画图方法(不要求证明).
,并简要说明画图方法(不要求证明).
如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长及H点的坐标;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积.
已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC,笔山职中数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PO的距离;(2)移动信号发射塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=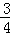 .
.
(1)求⊙O的半径长;
(2)求线段CF长.