(本题12分)
已知 的顶点
的顶点 ,
,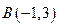
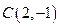 求:
求:
(1) 边上的中线所在的直线方程
边上的中线所在的直线方程
(2)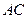 边上的高
边上的高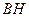 所在的直线方程.
所在的直线方程.
如图,在直三棱柱ABC-A1B1C1中,底面△ABC为等腰直角三角形,∠B = 900,D为棱BB1上一点,且面DA1 C⊥面AA1C1C.求证:D为棱BB1中点;(2) 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: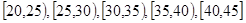 .
.
(I)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在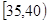 岁的人数;
岁的人数;
(II)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望. 
已知定圆 的圆心为
的圆心为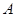 ,动圆
,动圆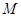 过点
过点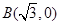 ,且和圆
,且和圆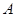 相切,动圆的圆心
相切,动圆的圆心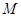 的轨迹记为
的轨迹记为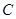 .
.
(Ⅰ)求曲线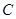 的方程;
的方程;
(Ⅱ)若点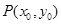 为曲线
为曲线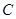 上一点,试探究直线:
上一点,试探究直线: 与曲线
与曲线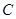 是否存在交点? 若存在,求出交点坐标;若不存在,请说明理由.
是否存在交点? 若存在,求出交点坐标;若不存在,请说明理由.
已知数列 中,
中,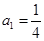 ,
,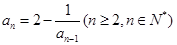 ,若数列
,若数列 满足
满足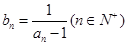 .
.
(Ⅰ)证明:数列 是等差数列,并写出
是等差数列,并写出 的通项公式;
的通项公式;
(Ⅱ)求数列 的通项公式及数列
的通项公式及数列 中的最大项与最小项.
中的最大项与最小项.
如图,多面体 中,四边形
中,四边形 是边长为
是边长为 的正方形,平面
的正方形,平面 垂直于平面
垂直于平面 ,且
,且 ,
, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 分别为棱
分别为棱 和
和 的中点,求证:
的中点,求证: ∥平面
∥平面 ;
;
(Ⅲ)求多面体 的体积.
的体积.