(本小题满分13分)
已知函数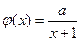 ,
,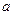 为正常数.
为正常数.
(1)若 ,且
,且 ,求函数
,求函数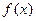 的单调增区间;
的单调增区间;
(2)若 ,且对任意
,且对任意 ,
,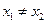 ,都有
,都有 ,求
,求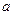 的的取值范围.
的的取值范围.
抛物线y2=2px(p>0)上纵坐标为-p的点M到焦点的距离为2.
(Ⅰ)求p的值;
(Ⅱ)如图,A,B,C为抛物线上三点,且线段MA,MB,MC 与x轴交点的横坐标依次组成公差为1的等差数列,若△AMB的面积是△BMC面积的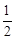 ,求直线MB的方程.
,求直线MB的方程.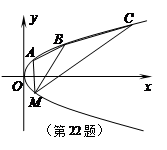
已知函数 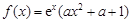
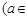 R).
R).
(Ⅰ)若 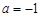 ,求曲线
,求曲线  在点
在点 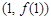 处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 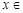
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知数列 {an} 是首项为 a1=1 的等差数列,其前n项和为Sn,数列 {bn} 是首项 b1=2 的等比数列,且 b2S2=16,b1b3=b4.
(Ⅰ)求数列 {an},{bn} 的通项公式;
(Ⅱ)若数列 {cn} 满足 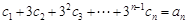 ,求数列 {cn} 的前n项和 Tn.
,求数列 {cn} 的前n项和 Tn.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,D为BC中点.
(Ⅰ) 求证:A1B//平面ADC1;
(Ⅱ) 求证:C1A⊥B1C;
(Ⅲ) 求直线B1C1与平面A1B1C所成的角.
设函数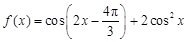 .
.
(Ⅰ)求 的最大值,并写出使
的最大值,并写出使 取最大值是
取最大值是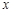 的集合;
的集合;
(Ⅱ)求 的单调递增区间;
的单调递增区间;
(Ⅲ)已知△ABC中,角A,B,C的对边分别为a,b,c.若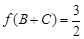 ,
,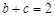 ,求a的最小值.
,求a的最小值.