已知数列 {an} 是首项为 a1=1 的等差数列,其前n项和为Sn,数列 {bn} 是首项 b1=2 的等比数列,且 b2S2=16,b1b3=b4.
(Ⅰ)求数列 {an},{bn} 的通项公式;
(Ⅱ)若数列 {cn} 满足 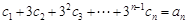 ,求数列 {cn} 的前n项和 Tn.
,求数列 {cn} 的前n项和 Tn.
如图,椭圆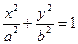 上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.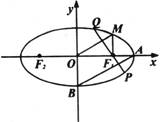
(1)求椭圆的离心率;
(2)F2是椭圆的左焦点,C是椭圆上的任一点,证明:
∠F1CF2≤ ;
(3)过F1且与AB垂直的直线交椭圆于P、Q,若△PF2Q的面积是20,求此时椭圆的方程.
设x,y∈R,i,j为直角坐标平面内x,y轴正方向上的单位向量,若向量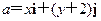 ,b=xi+(y-2)j,且|a|+|b|=8.
,b=xi+(y-2)j,且|a|+|b|=8.
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点,设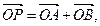 是否存在这样的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程;若不存在,试说明理由.
是否存在这样的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程;若不存在,试说明理由.
如题15图,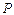 是抛物线
是抛物线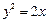 上的动点,点
上的动点,点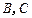 在
在 轴上,圆
轴上,圆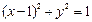 内切于
内切于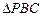 ,求
,求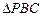 面积的最小值.
面积的最小值.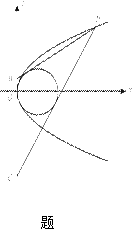
解不等式 .
.
已知函数 的图像与直线
的图像与直线
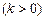 有且仅有三个交点,交点的横坐标的最大值为
有且仅有三个交点,交点的横坐标的最大值为 ,求证:
,求证:
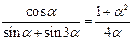 .
.