如图,椭圆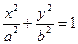 上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.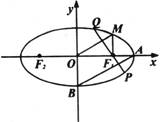
(1)求椭圆的离心率;
(2)F2是椭圆的左焦点,C是椭圆上的任一点,证明:
∠F1CF2≤ ;
(3)过F1且与AB垂直的直线交椭圆于P、Q,若△PF2Q的面积是20,求此时椭圆的方程.
(本题满分12分)
已知函数f(x)=x3+ax2+(a+6)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是3,求a,b的值;
(2)若f(x)为R上的单调递增函数,求a的取值范围.
(本小题满分12分)
已知数列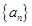 的首项为2,点
的首项为2,点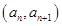 在函数
在函数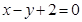 的图像上
的图像上
(Ⅰ)求数列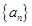 的通项公式;
的通项公式;
(Ⅱ)设数列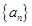 的前
的前 项之和为
项之和为 ,求
,求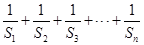 的值.
的值.
(本题14分)
设函数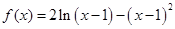 .
.
(1)求函数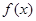 的单调递增区间;
的单调递增区间;
(2)若关于 的方程
的方程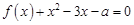 在区间
在区间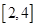 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数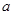 的取值范围.
的取值范围.
(本题12分)
已知函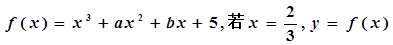 有极值,且曲线
有极值,且曲线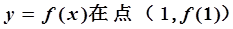 处的切线斜率为3.
处的切线斜率为3.
(1)求函数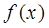 的解析式;
的解析式;
(2)求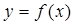 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函数 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
(本题12分)
在 中,角
中,角 所对的边为
所对的边为 已知
已知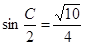 .
.
(1)求 的值;
的值;
(2)若 的面积为
的面积为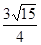 ,且
,且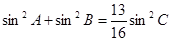 ,求
,求 的值.
的值.