(本题12分)
已知函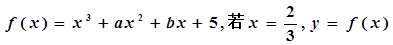 有极值,且曲线
有极值,且曲线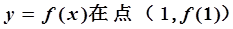 处的切线斜率为3.
处的切线斜率为3.
(1)求函数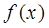 的解析式;
的解析式;
(2)求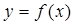 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函数 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
已知 ,其中
,其中 是自然常数,
是自然常数,
(1)讨论 时,
时,  的单调性、极值;
的单调性、极值;
(2)是否存在实数 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,又
上是减函数,又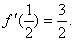 .
.
(1) 求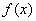 的解析式;
的解析式;
(2) 若在区间 (m>0)上恒有
(m>0)上恒有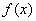 ≤x成立,求m的取值范围。
≤x成立,求m的取值范围。
已知抛物线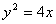 及点
及点 ,直线
,直线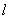 斜率为1且不过点
斜率为1且不过点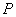 ,与抛物线交于点A,B,
,与抛物线交于点A,B,
(1) 求直线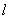 在
在 轴上截距的取值范围;
轴上截距的取值范围;
(2) 若AP,BP分别与抛物线交于另一点C、D,证明:AD,BC交于定点.
分别求适合下列条件圆锥曲线的标准方程:
(1)焦点为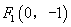 、
、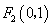 且过点
且过点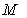
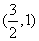 椭圆;
椭圆;
(2)与双曲线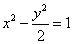 有相同的渐近线,且过点
有相同的渐近线,且过点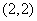 的双曲线.
的双曲线.
已知函数: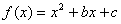 ,其中:
,其中: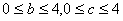 ,记函数
,记函数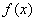 满足条件:
满足条件: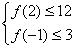 的事件为A,求事件A发生的概率。
的事件为A,求事件A发生的概率。