（本题14分）
设函数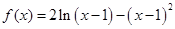
．
（1）求函数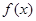
的单调递增区间；
（2）若关于
的方程
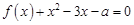在区间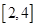
内恰有两个相异的实根，求实数
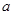的取值范围．
选修4-5：不等式选讲
已知x，y，z都是正数，且xyz = 1，求证：（1+x）（1+y）（1+z） ≥ 8.
选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知曲线C：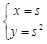
，直线l：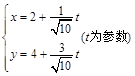
.设曲线C 与直线l交于A，B两点，求线段AB的长度.
选修4-2：矩阵与变换
已知矩阵
，A的逆矩阵
.
（1）求a，b的值；（2）求A的特征值.
选修4-1：几何证明选讲
如图，过点A的圆与BC切于点D，且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线，
求证：EF∥BC.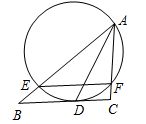
给定一个数列
，在这个数列里，任取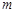
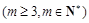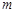项，并且不改变它们在数列中的先后次序，得到的数列的一个阶子数列.
已知数列的通项公式为
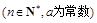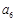，等差数列
，
，
是数列的一个3阶子数列.
（1）求
的值；
（2）等差数列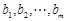
是的一个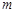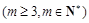阶子数列，且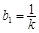
，求证：
；
（3）等比数列
是的一个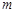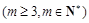阶子数列，求证：
.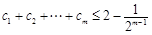