((本小题满分12分)
若图为一简单组合体,其底面ABCD为正方形,PD 平面ABCD,EC//PD,且PD=2EC。
平面ABCD,EC//PD,且PD=2EC。
(1)求证:BE//平面PDA;
(2)若N为线段PB的中点,求证:EN 平面PDB;
平面PDB;
(3)若 ,求平面PBE与平面ABCD所成的二面角的大小。
,求平面PBE与平面ABCD所成的二面角的大小。
(13分)已知圆O:x2+y2=3的半径等于椭圆E: =1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x-
=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x-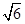 的距离为
的距离为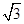 -
-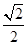 ,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
(1)求椭圆E的方程;
(2)求证:|AF|-|BF|=|BM|-|AM|.
已知函数f(x)=ln(x+1)-x2-x.
(1)若关于x的方程f(x)=-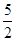 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
(2)证明:对任意的正整数n,不等式2+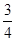 +
+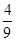 +…+
+…+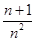 >ln(n+1)都成立.
>ln(n+1)都成立.
设函数f(x)=ln x+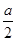 x2-(a+1)x(a>0,a为常数).
x2-(a+1)x(a>0,a为常数).
(1)讨论f(x)的单调性;
(2)若a=1,证明:当x>1时,f(x)<  x2-
x2-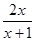 -
-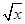 .
.
(13分)某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x),当年产量不足80千件时,C(x)=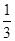 x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+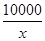 -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
如图1所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图2所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连接AB,设点F是AB的中点.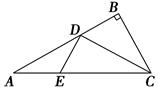
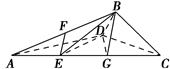
图1图2
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥BDEG的体积.