(本小题满分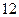 分)
分)
如图,在四棱柱ABCD—A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D= ,底面ABCD为直角梯形,其中BC//AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC//AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:A1O//平面AB1C;
(Ⅱ)求锐二面角A—C1D1—C的余弦值.
(本小题满分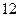 分)
分)
桌面上有两颗均匀的骰子(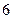 个面上分别标有数字
个面上分别标有数字 ).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为
).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为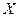 .
.
(Ⅰ)求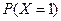 ;
;
(Ⅱ)求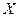 的分布列及期望
的分布列及期望 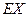 .
.
(本小题满分 分)
分)
设△ABC的内角A,B,C所对的边分别为 ,
, ,
, ,且
,且 。
。
(Ⅰ)求角A的大小;
(Ⅱ)若 =1,求△ABC的周长l的取值范围。
=1,求△ABC的周长l的取值范围。
.已知
(Ⅰ)如果函数 的单调递减区间为
的单调递减区间为 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)对一切的 ,
,

 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层, 每厘米厚的隔
每厘米厚的隔 热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=
热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0
(0 x
x 10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。