(本小题满分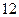 分)
分)
如图,在四棱柱ABCD—A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D= ,底面ABCD为直角梯形,其中BC//AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC//AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:A1O//平面AB1C;
(Ⅱ)求锐二面角A—C1D1—C的余弦值.
已知函数 .
.
(1)若 是函数,y=F(x)的极值点,求实数a的值;
是函数,y=F(x)的极值点,求实数a的值;
(2)若函数y=F(x)(x∈(0,3])的图象上任意一点处切线的斜率 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数y=f(x)在[1,2]上有两个零点,求实数a的取值范围.
如图所示的长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形,O为AC与BD的交点, ,M是线段B1D1的中点.
,M是线段B1D1的中点.
(1)求证:BM∥平面D1AC;
(2)求证:D1O⊥平面AB1C;
(3)求二面角B﹣AB1﹣C的大小.
某社区举办防控甲型H7N9流感知识有奖问答比赛,甲、乙、丙三人同时回答一道卫生知识题,三人回答正确与错误互不影响.已知甲回答这题正确的概率是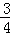 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是 .
.
(1)求乙、丙两人各自回答这道题正确的概率;
(2)用ξ表示回答该题正确的人数,求ξ的分布列和数学期望Eξ.
已知数列{an}满足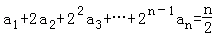 ,n∈N*.
,n∈N*.
(1)求数列{an}的通项公式;
(2)设bn=(2n﹣1)an,求数列{bn}的前n项和Sn.
在△ABC中,已知角A、B、C的对边分别为a、b、c.向量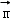 =(cosB,cosC),
=(cosB,cosC),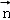 =(b,2a﹣c)且向量
=(b,2a﹣c)且向量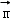 与
与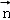 共线.
共线.
(1)求cosB的值;
(2)若b= ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.