.已知
(Ⅰ)如果函数 的单调递减区间为
的单调递减区间为 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)对一切的 ,
,

 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
已知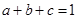 ,且
,且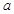 、
、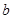 、
、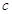 是正数,求证:
是正数,求证: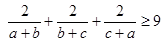 .
.
在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的极坐标方程 ,曲线C的参数方程为
,曲线C的参数方程为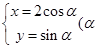 为参数),求曲线C截直线l所得的弦长。
为参数),求曲线C截直线l所得的弦长。
已知函数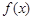 的导函数是
的导函数是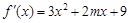 ,
,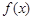 在
在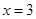 处取得极值,且
处取得极值,且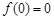 ,
,
(Ⅰ)求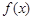 的极大值和极小值;
的极大值和极小值;
(Ⅱ)记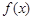 在闭区间
在闭区间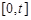 上的最大值为
上的最大值为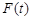 ,若对任意的
,若对任意的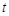
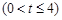 总有
总有 成立,求
成立,求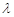 的取值范围;
的取值范围;
(Ⅲ)设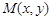 是曲线
是曲线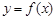 上的任意一点.当
上的任意一点.当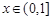 时,求直线OM斜率的最
时,求直线OM斜率的最
小值,据此判断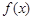 与
与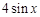 的大小关系,并说明理由.
的大小关系,并说明理由.
已知抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线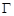 的方程;
的方程;
(Ⅱ)动直线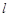 恒过点
恒过点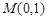 与抛物线
与抛物线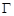 交于A、B两点,与
交于A、B两点,与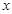 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(I)求证:A1C⊥平面BCDE;
(II)若M是A1D的中点,求CM与平面A1BE所成角的大小;