如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(I)求证:A1C⊥平面BCDE;
(II)若M是A1D的中点,求CM与平面A1BE所成角的大小;
(本小题满分14分)已知函数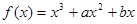 在
在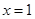 处有极值
处有极值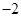 .
.
(1)求常数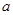 、
、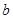 ;
;
(2)求曲线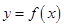 与
与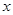 轴所包围的面积。
轴所包围的面积。
(本小题满分14分)某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过对市场的预测,当对两项投入都不大于3(百万元)时,每投入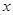 (百万元)广告费,增加的销售额可近似的用函数
(百万元)广告费,增加的销售额可近似的用函数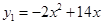 (百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数
(百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数 (百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)
(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)
(本小题满分12分)已知函数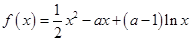 ,其中
,其中 ,讨论函数
,讨论函数 的单调性.
的单调性.
(本小题满分12分)已知函数 ,过点
,过点 作曲线
作曲线 的切线的方程,求切线方程.
的切线的方程,求切线方程.
(文).已知圆 及点
及点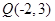 .
.
(1) 在圆上,求线段
在圆上,求线段 的长及直线
的长及直线 的斜率;
的斜率;
(2)若 为圆
为圆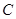 上任一点,求
上任一点,求 的最大值和最小值;
的最大值和最小值;
(3)若实数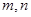 满足
满足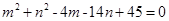 ,求
,求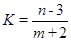 的最大值和最小值.
的最大值和最小值.