(本小题满分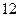 分)
分)
桌面上有两颗均匀的骰子(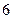 个面上分别标有数字
个面上分别标有数字 ).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为
).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为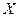 .
.
(Ⅰ)求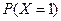 ;
;
(Ⅱ)求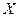 的分布列及期望
的分布列及期望 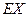 .
.
已知函数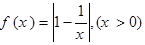
(1)当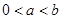 ,且
,且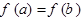 时,求证:
时,求证:
(2)是否存在实数 ,使得函数
,使得函数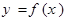 的定义域、值域都是
的定义域、值域都是 ?若存在,则求出
?若存在,则求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知函数
(1)若函数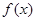 的值域为
的值域为 ,求实数
,求实数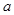 的取值范围;
的取值范围;
(2)当 时,函数
时,函数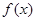 恒有意义,求实数
恒有意义,求实数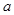 的取值范围.
的取值范围.
为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 与
与 的函数关系式为
的函数关系式为 (
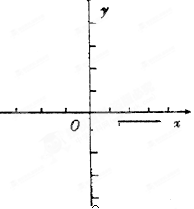
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: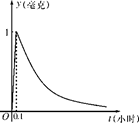
(1)求从药物释放开始,每立方米空气中的含药量 (毫克)与时间
(毫克)与时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室.那从药物释放开始,至少需要经过多少小时后,学生才能回到教室?
已知奇函数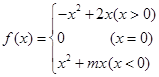
(1)求实数 的值,并在给出的直角坐标系中画出
的值,并在给出的直角坐标系中画出 的图象;
的图象;
(2)若函数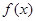 在区间
在区间 上单调递增,试确定实数
上单调递增,试确定实数 的取值范围.
的取值范围.
设集合 ,
,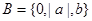 且
且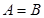 .
.
⑴求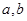 的值;
的值;
⑵判断函数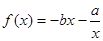 在
在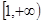 的单调性,并用定义加以证明.
的单调性,并用定义加以证明.