(13分)在中学阶段,对许多特定集合(如实数集、复数集以及平面向量集等)的学习常常是以定义运算(如四则运算)和研究运算律为主要内容.现设集合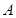 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在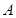 上定义一个运算,记为
上定义一个运算,记为 ,对于
,对于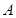 中的任意两个元素
中的任意两个元素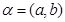 ,
, ,规定:
,规定:
 .
.
(1)计算: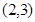

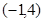 ;
;
(2)请用数学符号语言表述运算 满足交换律,并给出证明;
满足交换律,并给出证明;
(3)若“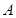 中的元素
中的元素 ”是“对
”是“对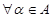 ,都有
,都有


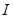

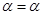 成立”的充要条件,试求出元素
成立”的充要条件,试求出元素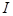 .
.
已知椭圆C: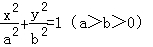 的离心率为
的离心率为 ,其中左焦点(﹣2,0).
,其中左焦点(﹣2,0).
(1)求椭圆C的方程;
(2)若直线y=x+m与椭圆C交于不同的两点A,B,求线段AB的最大值.
已知正方形ABCD,PA⊥平面ABCD,且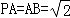 ,E是AB中点.
,E是AB中点.
(1)求证:AE⊥平面PBC;
(2)求点E到平面PAC的距离.
设定函数f(x)= x3+bx2+cx+d(a>0),且方程f′(x)﹣9x=0的两个根分别为1,4.
x3+bx2+cx+d(a>0),且方程f′(x)﹣9x=0的两个根分别为1,4.
(1)当a=3且曲线y=f(x)过原点时,求f(x)的解析式;
(2)若f(x)在(﹣∞,+∞)无极值点,求a的取值范围.
已知函数 的导数为
的导数为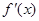 ,且数列
,且数列 满足
满足 .
.
(1)若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)若对任意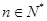 ,都有
,都有 ,成立
,成立 的取值范围.
的取值范围.
2013年我国汽车拥有量已超过2亿(目前只有中国和美国超过2亿),为了控制汽车尾气对环境的污染,国家鼓励和补贴购买小排量汽车的消费者,同时在部分地区采取对新车展限量上号.某市采取对新车限量上号政策,已知2013年年初汽车拥有量为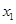 (
(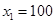 万辆),第
万辆),第 年(2013年为第1年,2014年为第2 年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2 年,依次类推)年初的拥有量记为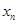 ,该年的增长量
,该年的增长量 和
和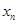 与
与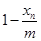 的乘积成正比,比例系数为
的乘积成正比,比例系数为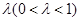 其中
其中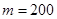 万.
万.
(1)证明: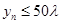 ;
;
(2)用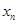 表示
表示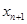 ;并说明该汽车总拥有量是否能控制在200万辆内.
;并说明该汽车总拥有量是否能控制在200万辆内.