((本小题满分12分)
已知椭圆的中心为坐标原点O,焦点在x轴上,椭圆短半轴长为1,动点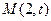
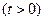 在直线
在直线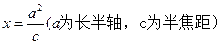 上。
上。
(1)求椭圆的标准方程
(2)求以OM为直径且被直线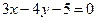 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值。
(本小题14分)已知函数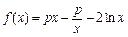 .
.
⑴若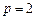 ,求曲线
,求曲线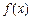 在点
在点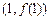 处的切线方程;
处的切线方程;
⑵若函数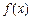 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数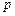 的取值范围;
的取值范围;
⑶设函数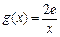 ,若在
,若在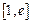 上至少存在一点
上至少存在一点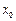 ,使得
,使得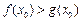 成立,求实数
成立,求实数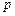 的取值范围.
的取值范围.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥1),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置
应在哪里?如果DE是参观线路,则希望它最长,DE的位置
又应在哪里?请予证明.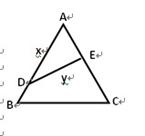
已知函数 的一系列对应值如下表:
的一系列对应值如下表: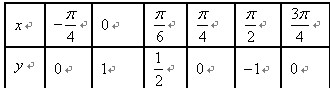
(1)求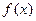 的解析式;
的解析式;
(2)若在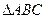 中,
中,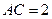 ,
,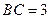 ,
,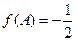 ,求
,求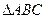 的面积.
的面积.
(12分)
在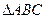 中,
中,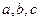 分别是
分别是 的对边长,已知
的对边长,已知 .
.
(1)若 ,求实数
,求实数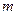 的值;
的值;
(2)若 ,求
,求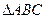 面积的最大值.
面积的最大值.
( 12分)已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y=0垂直。
(1)求实数a、b的值;(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.