（满分8分）
已知
是实数，函数
。
（I）若
，求的值；
（II）在（1）的条件下，求曲线
在点
处的切线方程；
（III）求
在区间
上的最大值。
（1）计算：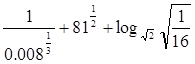
；
（2）解方程：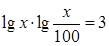
．
某食品厂定期收购面粉，已知该厂每天需要面粉6吨，每吨面粉的价格为1800元，面粉的保管等其他费用为平均每吨每天3元，购买面粉每次需支付运费900元.
（1）求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？
（2）若提供面粉的公司规定：当一次购买面粉不少于210吨时，其价格可享受9折优惠（即原价的90%），问该厂是否考虑利用此优惠条件？请说明理由.
已知中心在原点的双曲线
的右焦点为
，右顶点为
.
（1）求双曲线的方程；
（2）若直线
与双曲线恒有两个不同的交点
和
，且
（其中
为原点），求
的取值范围.
已知函数
在
处有极值，其图像在
处的切线与直线
平行.
（1）求函数的单调区间；
（2）当
时，
恒成立，求实数
的取值范围.
命题
方程
是焦点在
轴上的椭圆，命题
函数
在
上单调递增.若
为假，
为真，求实数
的取值范围.