(本小题满分15分)
某企业有两个生产车间分别在A,B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A,B,C中任意两点间的距离均有1 km,设∠BDC=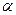 ,所有员工从车间到食堂步行的总路程为S.
,所有员工从车间到食堂步行的总路程为S.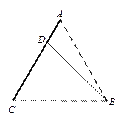
(1)写出S关于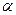 的函数表达式,并指出
的函数表达式,并指出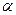 的取值范围;
的取值范围;
(2)问食堂D建在距离A多远时,可使总路程S最少?
(14分)设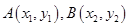 是椭圆
是椭圆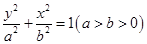 的两点,
的两点,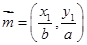 ,
,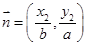 ,且
,且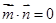 ,椭圆离心率
,椭圆离心率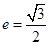 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1) 求椭圆方程;
(2) 若存在斜率为 的直线AB过椭圆的焦点
的直线AB过椭圆的焦点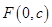 (
(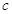 为半焦距),求
为半焦距),求 的值;
的值;
(3) 试问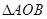 的面积是否为定值?若是,求出该定值;若不是,
的面积是否为定值?若是,求出该定值;若不是, 说明理由。
说明理由。
(13分)已知数列{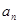 }的前n项和Sn=-
}的前n项和Sn=-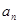 -
-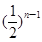 +2(n为正整数).
+2(n为正整数).
(1)令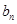 =
=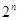
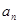 ,求证数列{
,求证数列{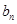 }是等差数列,并求数列{
}是等差数列,并求数列{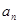 }的通项公式;
}的通项公式;
(2)令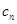 =
=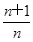
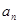 ,若Tn=c1+c2+…+cn, 求Tn。
,若Tn=c1+c2+…+cn, 求Tn。
(12分) 设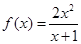 ,
,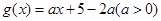 .
.
(1)求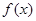 在
在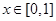 上的值域;
上的值域;
(2)若对于任意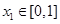 ,总存在
,总存在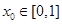 ,使得
,使得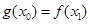 成立,求
成立,求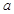 的取值范围.
的取值范围.
(12分) 如图,正三棱柱 中,
中, 是
是 的中点,
的中点,
(1)求证: ∥平面
∥平面 ;
;
(2)求二面角 的大小.
的大小.
(12分) 已知 的面积
的面积 其中
其中 分别为角
分别为角 所对的边.
所对的边.
(1)求角 的大小;(2)若
的大小;(2)若 ,求
,求 的最大值.
的最大值.