第十一届西博会于2010年10月22日至26日在蓉举行,本届西博会以“绿色改变生活,技术引领发展”为主题。如此重要的国际盛会,自然少不了志愿者这支重要力量,“志愿者,西博会最亮丽的风景线”,通过他们的努力和付出,已把志愿者服务精神的种子播撒到人们心中。某大学对参加了本次西博会的该校志愿者实施“社会教育实践”学分考核,因该批志愿者表现良好,该大学决定考核只有合格和优秀两个等次,若某志愿者考核为合格,授予0.5个学分;考核为优秀,授予1个学分。假设该校志愿者甲、乙、丙考核为优秀的概率分别为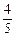 、
、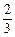 、
、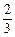 ,他们考核所得的等次相互独立。
,他们考核所得的等次相互独立。
(I)求在这次考核中,志愿者甲、乙、两三人中至少有一名考核为优秀的概率;
(II)求在这次考核中甲、乙、丙三名志愿者所得学分之和为整数的概率。
某家庭电话在家中有人时,打进的电话响第一声时被接的概率为0.1,响第二声时被接的概率为O.3,响第三声时被接的概率为0.4,响第四声时被接的概率为0.1,那么电话在响前4声内被接的概率是多少?
甲投篮命中率为O.8,乙投篮命中率为0.7,每人投3次,两人恰好都命中2次的概率是多少?
已知函数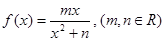 在
在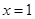 处取得极小值2.
处取得极小值2.
(1)求函数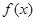 的解析式;
的解析式;
(2)求函数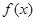 的极值;
的极值;
(3)设函数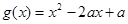 ,若对于任意
,若对于任意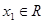 ,总存在
,总存在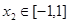 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
已知椭圆 过点
过点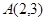 ,且离心率
,且离心率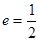 .
.
(1)求椭圆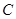 的标准方程;
的标准方程;
(2)是否存在过点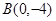 的直线
的直线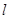 交椭圆于不同的两点M、N,且满足
交椭圆于不同的两点M、N,且满足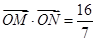 (其中点O为坐标原点),若存在,求出直线
(其中点O为坐标原点),若存在,求出直线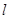 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
如图所示,在四棱锥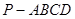 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面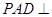 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.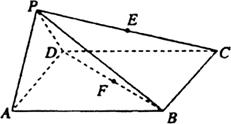
(1)求证: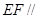 平面PAD;
平面PAD;
(2)求证:平面PDC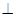 平面PAD;
平面PAD;
(3)求四棱锥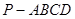 的体积.
的体积.