(本小题满分12分)
已知三棱柱 ,底面三角形
,底面三角形 为正三角形,侧棱
为正三角形,侧棱
 底面
底面 ,
,  ,
, 为
为 的中点,
的中点, 为
为 中点.
中点.
(Ⅰ) 求证:直线 平面
平面 ;
;
(Ⅱ)求平面 和平面
和平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题共12分)如图,三棱柱 中,侧面
中,侧面
 底面
底面 ,
, ,且
,且 ,O为
,O为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点 的位置.
的位置.
(本小题共12分)某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在的地区附近有A,B,C三家社区医院,并且他们对社区医院的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
(本小题共12分)已知向量
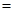
 ,
,
 ,
, .
.
(1)若 ,求
,求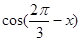 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是a,b, 且满足
且满足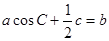 ,求函数
,求函数 的取值范围.
的取值范围.
已知函数 ,设
,设 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数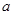 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
某厂家拟对一商品举行促 销活动,当该商品的售价为
销活动,当该商品的售价为 元时,全年的促销费用为
元时,全年的促销费用为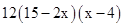 万元;根据以往的销售经验,实施促销后的年销售量
万元;根据以往的销售经验,实施促销后的年销售量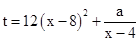 万件,其中4
万件,其中4 为常数.当该商品的售价为6元时,年销售量为49万件.
为常数.当该商品的售价为6元时,年销售量为49万件.
(Ⅰ)求出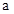 的值;
的值;
(Ⅱ)若每件该商品的成本为4元时,写出厂家销售该商品的年利润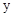 万元与售价
万元与售价 元之间的关系;
元之间的关系;
(Ⅲ)当该商品售价为多少元时,使厂家销售该商品所获年利润最大.