已知椭圆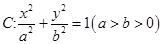 过点
过点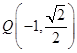 ,且离心率
,且离心率 .
.
(1)求椭圆C的方程;
(2)已知过点 的直线
的直线 与该椭圆相交于A、B两点,试问:在直线
与该椭圆相交于A、B两点,试问:在直线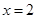 上是否存在点P,使得
上是否存在点P,使得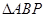 是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(本小题满分12分)正方形 与梯形
与梯形 所在平面互相垂直,
所在平面互相垂直, ,点
,点 在线段
在线段 上且不与
上且不与 重合.
重合.
(Ⅰ)当点 是
是 中点时,求证:
中点时,求证: ;
;
(Ⅱ)当平面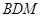 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求三棱锥
时,求三棱锥 的体积.
的体积.
(本小题满分12分)某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调 查结果如下表所示:
(Ⅰ)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(Ⅱ)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附: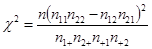 .
.
(本小题满分12分)设数列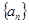 的各项均为正数,它的前
的各项均为正数,它的前 项和为
项和为 ,点
,点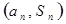 在函数
在函数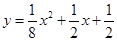 的图像上;数列
的图像上;数列 满足
满足 ,其中
,其中 .
.
(Ⅰ)求数列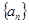 和
和 的通项公式;
的通项公式;
(Ⅱ)设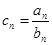 ,求证:数列
,求证:数列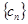 的前
的前 项和
项和 .
.
选修4-5:不等式证明选讲
已知 .
.
(1)解不等式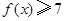 ;
;
(2)若关于 的不等式
的不等式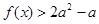 对任意的
对任意的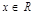 恒成立,求
恒成立,求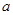 的取值范围.
的取值范围.
选修4-4:坐标系与参数方程
在平面直角坐标系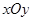 中,以坐标原点为极点,
中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线 ,曲线
,曲线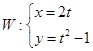 (
(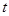 是参数).
是参数).
求直线 的直角坐标方程与曲线
的直角坐标方程与曲线 的普通方程;
的普通方程;
若点P在直线 上,Q在曲线
上,Q在曲线 上,求
上,求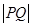 的最小值.
的最小值.