已知函数 在
在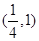 上的最大值为
上的最大值为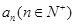
求数列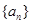 的通项公式;
的通项公式;
求证:对任何正整数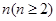 ,都有
,都有 ;
;
设数列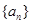 的前
的前 项和
项和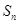 ,求证:对任何正整数
,求证:对任何正整数 ,都有
,都有 成立
成立
已知关于x的不等式 的解集不是空集.
的解集不是空集.
(1)求参数m的取值范围的集合M;
(2)设a,b M,求证:a+b<ab+1.
M,求证:a+b<ab+1.
已知曲线C的极坐标方程为 =2,以极点为原点,极轴为x轴的正半轴建立直角坐标系,P是曲线C上的动点,点A(2,0),M是线段AP的中点。
=2,以极点为原点,极轴为x轴的正半轴建立直角坐标系,P是曲线C上的动点,点A(2,0),M是线段AP的中点。
(1)求点M轨迹的直角坐标方程;
(2)求证点M到点E( ,0)、F(3、0)的距离之比是常数。
,0)、F(3、0)的距离之比是常数。
如图,AB是⊙O的一条直径,过A作⊙O的切线,在切线上取一点C,使AC=AB,连接OC,与⊙O交于点D,BD的延长线与AC交于点E,求证:
(1)∠CDE = ∠DAE
(2)AE = CD
已知函数f(x)=ex-e-x(x R)
R)
(1)求证:当x≥0时, ;
;
(2)试讨论函数H(x)=f(x)-ax(x R)的零点个数.
R)的零点个数.
已知直线x+y-1=0经过椭圆C:  的顶点和焦点F.
的顶点和焦点F.
(1)求此椭圆的标准方程;
(2)斜率为k,且过点F的动直线 与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证:直线BD过顶点.
与椭圆C交于A,B两点,点A关于x轴的对称点为D,求证:直线BD过顶点.