(本小题满分14分)已知定义在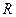 上的函数
上的函数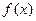 ,满足条件:①
,满足条件:①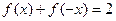 ,②对非零实数
,②对非零实数 ,都有
,都有 .
.
(1)求函数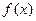 的解析式;
的解析式;
(2)设函数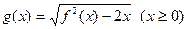 ,直线
,直线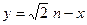 分别与函数
分别与函数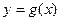 ,
, 交于
交于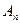 、
、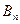 两点,(其中
两点,(其中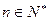 );设
);设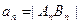 ,
, 为数列
为数列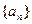 的前
的前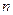 项和,求证:当
项和,求证:当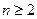 时,
时,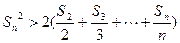 .
.
设数列{ }的前n项和为
}的前n项和为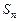 ,且
,且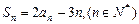 .
.
⑴证明数列{ }为等比数列
}为等比数列
⑵求{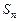 }的前n项和
}的前n项和
已知椭圆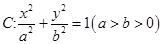 过点
过点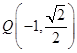 ,且离心率
,且离心率 .
.
(1)求椭圆C的方程;
(2)已知过点 的直线
的直线 与该椭圆相交于A、B两点,试问:在直线
与该椭圆相交于A、B两点,试问:在直线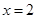 上是否存在点P,使得
上是否存在点P,使得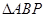 是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
已知函数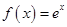 .
.
(1)当 时,设
时,设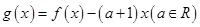 .讨论函数
.讨论函数 的单调性;
的单调性;
(2)证明当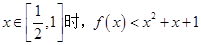 .
.
如图,在梯形ABCD中,AB//CD,AD=DC=CB=a,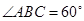 ,四边形ACFE是矩形,且平面
,四边形ACFE是矩形,且平面 平面ABCD,点M在线段EF上.
平面ABCD,点M在线段EF上.
(1)求证: 平面ACFE;
平面ACFE;
(2)当EM为何值时,AM//平面BDF?证明你的结论.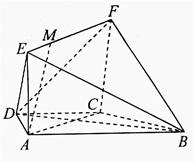
已知等差数列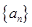 的首项
的首项 ,公差
,公差 ,数列
,数列 是等比数列,且
是等比数列,且 .
.
(1)求数列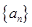 和
和 的通项公式;
的通项公式;
(2)设数列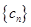 对任意正整数n,均有
对任意正整数n,均有 成立,求
成立,求 的值.
的值.