(本小题满分15分)
已知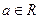 ,函数
,函数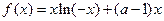 .
.
(Ⅰ)若 在
在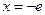 处取得极值,求函数
处取得极值,求函数 的单调区间;
的单调区间;
(Ⅱ)求函数 在区间
在区间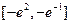 上的最大值
上的最大值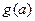 .(注:
.(注: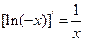 )
)
(本题12分)
求满足下列条件的直线方程:
(1)过点(2,3),斜率是直线 斜率的一半;
斜率的一半;
(2)过点(1,0),且过直线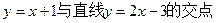
(本题12分)
已知直线
(1)若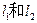 平行,求
平行,求 的值。
的值。
(2)若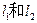 垂直,求
垂直,求 的值。
的值。
(本小题满分14分)
已知数列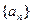 的前
的前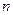 项和为
项和为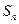 ,且
,且 .
.
(1)求数列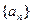 的通项公式;
的通项公式;
(2)设数列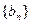 满足:
满足: ,求证:
,求证: ;
;
(3)求证: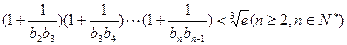 ]
]
(本小题满分13分)
已知函数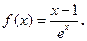
(1) 求函数 的单调区间和极值;
的单调区间和极值;
(2) 若函数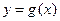 对任意
对任意 满足
满足 ,求证:当
,求证:当 ,
,
(3) 若 ,且
,且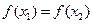 ,求证:
,求证: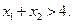
(本小题满分12分)
某商店储存的50个灯泡中, 甲厂生产的灯泡占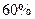 , 乙厂生产的灯泡占
, 乙厂生产的灯泡占 , 甲厂生产的灯泡的一等品率是
, 甲厂生产的灯泡的一等品率是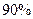 , 乙厂生产的灯泡的一等品率是
, 乙厂生产的灯泡的一等品率是 .
.
(1) 若从这50个灯泡中随机抽取出一个灯泡(每个灯泡被取出的机会均等), 则它是甲厂生产的一等品的概率是多少?
(2) 从这50个灯泡中随机抽取出的一个灯泡是一等品, 求它是甲厂生产的概率是 多少?
多少?
(3) 若从这50个灯泡中随机抽取出两个灯泡(每个灯泡被取出的机会均等), 这两个灯泡中是甲厂生产的一等品的个数记为 , 求
, 求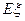 的值.
的值.