如图,在四棱锥 中,底面
中,底面 是边长为1的菱形,
是边长为1的菱形,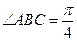 ,
,  底面
底面 ,
,  ,
, 为
为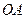 的中点.
的中点.
(Ⅰ)、求异面直线AB与MD所成角的大小;
(Ⅱ)、求平面 与平面
与平面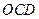 所成的二面角的余弦值.
所成的二面角的余弦值.
已知向量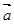 与
与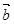 的夹角为
的夹角为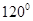 ,
,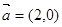 ,
,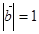 ,求
,求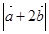 的值.
的值.
已知函数 .
.
(Ⅰ)若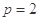 ,求曲线
,求曲线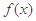 在点
在点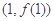 处的切线方程;
处的切线方程;
(Ⅱ)若函数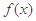 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(Ⅲ)若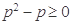 ,且至少存在一点
,且至少存在一点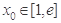 ,使得
,使得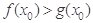 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆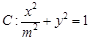 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆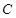 的方程;
的方程;
(Ⅱ)设直线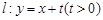 与椭圆
与椭圆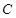 交于
交于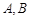 两点.若原点
两点.若原点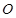 在以线段
在以线段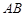 为直径的圆内,
为直径的圆内,
求实数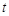 的取值范围.
的取值范围.
设数列 的各项都为正数,其前
的各项都为正数,其前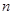 项和为
项和为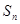 ,已知对任意
,已知对任意 ,
,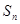 是
是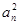 和
和 的等差中项.
的等差中项.
(Ⅰ)证明数列 为等差数列,并求数列
为等差数列,并求数列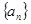 的通项公式;
的通项公式;
(Ⅱ)证明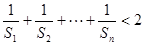 .
.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°.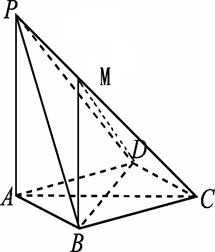
(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)求直线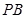 与平面
与平面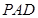 所成角的正切值;
所成角的正切值;
(Ⅲ)已知M在线段PC上,且BM=DM=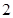 ,CM=3,求二面角
,CM=3,求二面角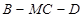 的余弦值.
的余弦值.