如图所示，BC是半径为R的1/4圆弧形光滑绝缘轨道，轨道位于竖直平面内，
其下端与水平绝缘轨道平滑连接，接个轨道处在水平向左的匀强电场中，电场强度为E。现有一质量为m的带电小滑块甲（体积很小可视为质点），在BC轨道的D点释放后静止不动。
已知OD与竖直方向的夹角为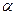
=37°，随后把它从C点由静止释放，滑到水平轨道上的A点时速度减为零。若已知滑块与水平轨道间的动摩擦因数为μ=0.25，且tan37°=0.75。求：
(1) 滑块甲的带电量q1和电性；
(2) 滑块下滑通过B点时的速度大小vB；
(3) 水平轨道上A、B两点之间的距离L：
(4) 现在B处放置一个质量与甲相同的带电滑块乙：然后还让甲从C点由静止释放，在B点与刚由静止释放的乙发生碰撞，碰后粘合在一起沿水平轨道上做匀速运动。忽略甲、乙之间的静电力作用，求碰后的共两速度v和碰前乙滑块的带电量q2及电性。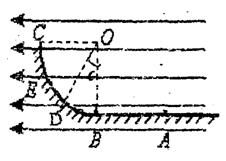
①对于定量气体，可能发生的过程是
| A．等压压缩，温度降低 | B．等温吸热，体积不变 |
| C．放出热量，内能增加 | D．绝热压缩，内能不变 |
②如图所示，有一个直立的气缸，气缸底到气缸口的距离为L0cm，用一厚度和质量均可忽略不计的刚性活塞A，把一定质量的空气封在气缸内，活塞与气缸间的摩擦可忽略，平衡时活塞上表面与气缸口的距离很小（计算时可忽略不计），周围大气的压强为H0cmHg。现把盛有水银的一个瓶子放在活塞上（瓶子的质量可忽略），平衡时活塞到气缸底的距离为Lcm。若不是把这瓶水银放在活塞上，而是把瓶内水银缓缓不断地倒在活塞上方，这时活塞向下移压缩气体，直到
活塞不再下移，求此时活塞在气缸内可能的位置以及与之相对应的条件（即题中给出量之间应满足的关系），设气体的温度不变。
如图所示，挡板P固定在足够高的水平桌面上，小物块A和B的大小可忽略，它们分别带有+QA和+QB的电荷量，质量分别为mA和mB。两物块由绝缘的轻弹簧相连，一不可伸长的轻绳跨过滑轮，一端与B连接，另一端连接轻质小钩。整个装置处于电场强度为E、方向水平向左的匀强电场中。A、B开始时静止，已知弹簧的劲度系数为k，不计一切摩擦及A、B间的库仑力，且设A、B所带电
荷量保持不变，B不会碰到滑轮。
①若在小钩上挂一质量为M的物块C并由静止释放，可使物块A
恰好能离开挡板P，求物块C下落的最大距离。
②若物块C的质量改为2M,则当物块A刚离开挡板P时，B的速度为多大？
有一方向如图的匀强电场和匀强磁场共存的场区，宽度d＝8 cm，一带电粒子（
不计重力）沿垂直电场线和磁感线方向射入场区后，恰可做直线运动，若撤去磁场，带电粒子穿过场区后向下侧移了y1="3.2" cm．若撤去电场，求带电粒子穿
过场区后的侧移量y2?
一个边长为a=1m的正方形线圈，总电阻为 R="0.1" Ω，当线圈以v =" 2" m/s的速度通过磁感强度B =" 0.5" T的匀强磁场区域时，线圈平面总保持与磁场垂直．若磁场的宽度b＞1 m，如图所示，求线圈通过磁场后释放多少焦耳的热量? 
如图所示，导体杆ab质量为m，电阻为R，放在与水平面夹角为θ的倾斜金属导轨上，导轨间距为d，电阻不计，系统处在竖直向上的匀强磁场中，磁感应强度为B，电池内阻不计.问：导体光滑时E为多大能使导体杆静止在导轨上？