已知函数 ,在点(1,f(1))处的切线方程为y+2=0.
,在点(1,f(1))处的切线方程为y+2=0.
(1) 求函数f(x)的解析式;
(2) 若对于区间[一2,2]上任意两个自变量的值x1,x2,都有 ,求实
,求实
数c的最小值;
(3) 若过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线,求实数m的取值范围,
(本小题满分12分)函数f(x)=loga(x2-4ax+3a2), 0<a<1, 当x∈[a+2,a+3]时,恒有|f(x)|≤1,试确定a的取值范围.
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重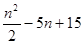 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为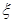 ,求E
,求E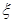 .
.
(本小题满分12分)已知集合A={x∣x2-3(a+1)x+2(3a+1)<0},B=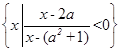 ,
,
(1)当a=2时,求A∩B;
(2)求使BÍA的实数a的取值范围.
(本小题满分12分)已知,如图,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交直线AC于点E,交AD于点F,过G作⊙O的切线,切点为H.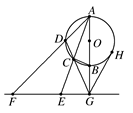
求证:(1)C,D,F,E四点共圆;
(2)GH2=GE·GF.
(本小题满分10分)某班主任对班级22名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多.
(1)根据以上数据建立一个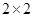 列联表;
列联表;
(2)试问喜欢电脑游戏与认为作业多少是否有关系?