(本小题满分12分)
已知函数 .
.
(1)设 ,求函数
,求函数 的极值;
的极值;
(2)若 ,且当
,且当 时,
时,
 12a恒成立,试确定
12a恒成立,试确定 的取值范围.
的取值范围.
(本题满分12分) 在 中,
中,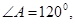
(Ⅰ)若三边长构成公差为4的等差数列,求 的面积
的面积
(Ⅱ)已知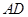 是
是 的中线,若
的中线,若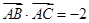 ,求
,求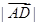 的最小值
的最小值
(本题满分12分)设函数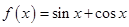 ,
,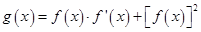
(Ⅰ)求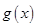 的周期和最大值
的周期和最大值
(Ⅱ)求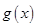 的单调递增区间
的单调递增区间
(本小题满分14分)
已知函数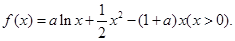
(1)求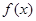 的单调区间;
的单调区间;
(2)若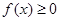 在
在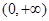 内恒成立,求实数a的取值范围;
内恒成立,求实数a的取值范围;
(3)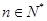 ,求证:
,求证: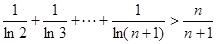
(本小题满分12分)
已知椭圆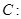
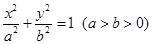 的离心率为
的离心率为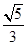 ,定点
,定点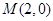 ,椭圆短轴的端点是
,椭圆短轴的端点是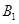 ,
,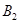 ,且
,且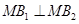 .
.
(Ⅰ)求椭圆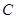 的方程;
的方程;
(Ⅱ)设过点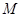 且斜率不为
且斜率不为 的直线交椭圆
的直线交椭圆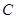 于
于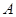 ,
,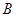 两点.试问
两点.试问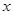 轴上是否存在定点
轴上是否存在定点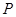 ,使
,使 平分
平分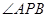 ?若存在,求出点
?若存在,求出点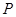 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: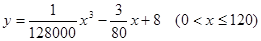 .已知甲、乙两地相距100千米。
.已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?