金属圆环半径r1=10m,内有半径为r2= 的圆形磁场磁感强度随时间的变化关系如图乙,金属圆环与电容C、电阻及平行金属板MN如图甲连接,金属圆环电阻为r0=2Ω,R1=R3=3Ω,R2=R5=2Ω,R4=7Ω,紧靠MN的右侧有一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB以外都是光滑的。其中AB与BC轨道以微小圆弧相接。一个绝缘带电小球以初速度V0=4.0m/s从MN左侧紧靠上极板(不接触)水平飞入,从A点飞出电场速度恰好沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数u=0.50。(g取10m/s2,sin37°="0.60," cos37°="0.80)" ,
的圆形磁场磁感强度随时间的变化关系如图乙,金属圆环与电容C、电阻及平行金属板MN如图甲连接,金属圆环电阻为r0=2Ω,R1=R3=3Ω,R2=R5=2Ω,R4=7Ω,紧靠MN的右侧有一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB以外都是光滑的。其中AB与BC轨道以微小圆弧相接。一个绝缘带电小球以初速度V0=4.0m/s从MN左侧紧靠上极板(不接触)水平飞入,从A点飞出电场速度恰好沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数u=0.50。(g取10m/s2,sin37°="0.60," cos37°="0.80)" ,

(1)平行金属板MN两端电压是多少?
(2)为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件?
(3)按照(2)的要求,小物块进入轨道后可以有多少次通过圆轨道上距水平轨道高为0.01m的某一点。
(8分)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止释放,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,可测出相应的N的大小,N随H的变化关系如图乙折线PQI所示(PQ与QI两直线相连接于Q点),QI反向延长交纵轴于F点(0,5.8N),重力加速度g取10m/s2,求: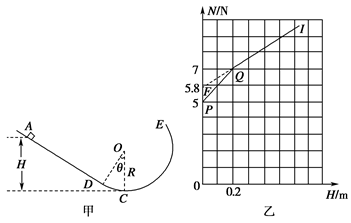
(1)图线上的PQ段是对应物块在哪段轨道上由静止释放(无需说明理由)?并求出小物块的质量m;
(2)圆轨道的半径R、轨道DC所对应的圆心角θ;
(3)小物块与斜面AD间的动摩擦因数μ。
(8分)山地滑雪是人们喜爱的一项体育运动,一滑雪坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=5 m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差h=8.8 m,运动员连同滑雪装备总质量为80 kg,从A点由静止滑下通过C点后飞落(不计空气阻力和轨道的摩擦阻力,g取10 m/s2,sin37°=0.6,cos37°=0.8).求:
(1)运动员到达C点的速度大小;
(2)运动员经过C点时轨道受到的压力大小.
(8分) “嫦娥一号”的成功发射,为实现中华民族几千年的奔月梦想迈出了重要的一步。已知“嫦娥一号”绕月飞行轨道近似为圆形,距月球表面高度为H,飞行周期为T,月球的半径为R,引力常量为G。求:
(1)“嫦娥一号”绕月飞行时的线速度大小;
(2)月球的质量;
(3)若发射一颗绕月球表面做匀速圆周运动的飞船,则其绕月运行的线速度应为多大。
(6分)质量为500吨的机车以恒定的功率由静止出发,经5min行驶2. 25km,速度达到最大值54km/h,设阻力恒定。问:(1)机车的功率P多大?(2)机车的速度为36 km/h时机车的加速度a多大?
(6分)人拉原来静止的重300N的车在水平路面上前进,拉力大小为20N,方向斜向上且与水平方向成300角,车前进500米,车与路面的动摩擦因数为0.03,求:
(1)拉力对车所做的功;
(2)摩擦力对车所做的功;
(3)车获得的动能.