(8分)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止释放,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,可测出相应的N的大小,N随H的变化关系如图乙折线PQI所示(PQ与QI两直线相连接于Q点),QI反向延长交纵轴于F点(0,5.8N),重力加速度g取10m/s2,求: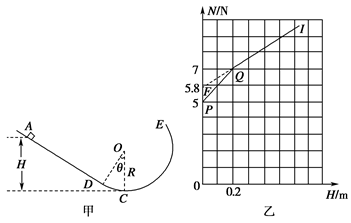
(1)图线上的PQ段是对应物块在哪段轨道上由静止释放(无需说明理由)?并求出小物块的质量m;
(2)圆轨道的半径R、轨道DC所对应的圆心角θ;
(3)小物块与斜面AD间的动摩擦因数μ。
宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用。现已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆轨道上运行。设每个星体的质量均为m。万有引力常量为G。
(1)试求第一种形式下,星体运动的线速度大小和周期;
(2)假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?
如图所示,在x>0的空间中,存在沿x轴正方向的匀强电场E;在x<0的空间中,存在沿x轴负方向的匀强电场,场强大小也为E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度V0开始运动,不计电子重力.求:
(1)电子的x方向分运动的周期.
(2)电子运动的轨迹与y轴的各个交点中,任意两个交点的距离.
如图,将一个物体轻放在倾角为θ=45°足够长的粗糙斜面上,同时用一个竖直向上逐渐增大的力F拉物体,其加速度大小a随外力F大小变化的关系如图,试由图中所给的信息求:(g取10m/s2,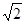 取1.4)
取1.4)
⑴斜面的动摩擦因数μ;
⑵当加速度大小a =" 2.1" m/s2时,外力F的大小。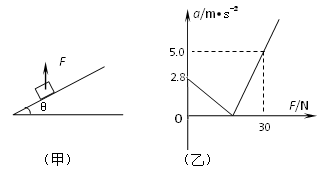
如图甲所示,水平放置的平行金属板A、B,两板的中央各有一小孔O1、O2,板间距离为d,当t=0时,在a、b两端加上如图乙所示的电压,同时,在c、d两端加上如图丙所示的电压.此时将开关S接1.一质量为m的带负电微粒P恰好静止于两孔连线的中点处(P、O1、O2在同一竖直线上).重力加速度为g,不计空气阻力.
(1)若在t=T/4时刻,将开关S从1扳到2,当Ucd=2U0时,求微粒P加速度的大小和方向;
(2)若要使微粒P以最大的动能从A板的小孔O1射出,问在t=T/2到t=T之间的哪个时刻,把开关S从1扳到2?Ucd的周期T至少为多少?
AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平,一个质量为m的小物块P从轨道顶端A处静止释放,滑到B端后飞出,落到地面上的点C,已知它落地相对于点B的水平位移 。现在轨道下方紧贴点B安装一水平传送带,传送带的右端与B间的距离为
。现在轨道下方紧贴点B安装一水平传送带,传送带的右端与B间的距离为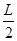 ,当传送带静止时让物体P再次从点A由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的点C。取g=10m/s2
,当传送带静止时让物体P再次从点A由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的点C。取g=10m/s2
(1)求物体P滑至B点时的速度大小;(2)求物体P与传送带之间的动摩擦因数;
(3)若皮带轮缘以 的线速度顺时针匀速转动,求物体落点到O点的距离。
的线速度顺时针匀速转动,求物体落点到O点的距离。