(本小题满分15分)
如图,椭圆方程为
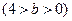 ,
, 为椭圆上的动点,
为椭圆上的动点,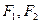 为椭圆的两焦点,当
为椭圆的两焦点,当 点不在
点不在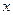 轴上时,过
轴上时,过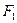 作
作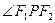 的外角平分线的垂线
的外角平分线的垂线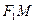 ,垂足为
,垂足为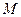 ,当点
,当点 在
在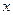 轴上时,定义
轴上时,定义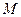 与
与 重合。
重合。
(Ⅰ)求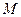 点的轨迹
点的轨迹 的方程;
的方程;
(Ⅱ)已知 、
、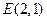 ,试探究是否存在这样的点
,试探究是否存在这样的点 :点
:点 是轨迹
是轨迹 内部的整点(平面内横、纵坐标均为整数的点称为整点),且
内部的整点(平面内横、纵坐标均为整数的点称为整点),且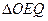 的面积
的面积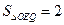 ?若存
?若存 在,求出点
在,求出点 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l经过点P( ,1),倾斜角α=
,1),倾斜角α= ,圆C的极坐标方程为
,圆C的极坐标方程为 =
=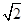 cos(θ-
cos(θ-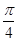 ).
).
(Ⅰ)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(Ⅱ)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积.
(本小题满分10分)选修4—1:几何证明选讲如图,四边形ACED是圆内接四边形,AD、CE的延长线交于点B,且AD=DE,AB=2AC.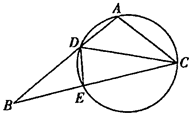
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.
(本小题满分12分)
已知函数f(x)=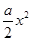 -bx+lnx(a,b∈R).
-bx+lnx(a,b∈R).
(Ⅰ)若a=b=1,求f(x)点(1,f(1))处的切线方程;
(Ⅱ)设a<0,求f(x)的单调区间;
(Ⅲ)设a<0,且对任意的x>0,f(x)≤f(2),试比较ln(-a)与-2b的大小.
(本小题满分12分)已知直线l:y=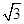 x-2
x-2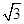 过椭圆C:
过椭圆C: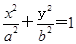 (a>b>0)的右焦点,且椭圆的离心率为
(a>b>0)的右焦点,且椭圆的离心率为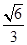 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,1)的直线与椭圆C交于点A,B,求△AOB的面积的最大值.
(本小题满分12分)如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.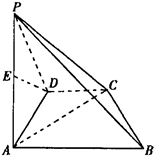
(Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求三棱锥A-PBC的体积.