(本题14分)如图,在四棱锥 中,底面
中,底面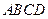 是边长为1的菱形,
是边长为1的菱形, ,
,  ,
, 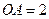 ,
, 为
为 的中点,
的中点, 为
为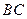 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)求异面直线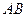 与
与 所成角的大小;
所成角的大小;
(Ⅲ)求点 到平面
到平面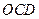 的距离.
的距离.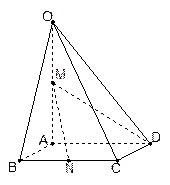
圆C的圆心在y轴上,且与两直线m1: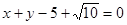 ;m2:
;m2: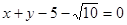 均相切.
均相切.
(I)求圆C的方程;
(II)过抛物线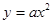 上一点M,作圆C的一条切线ME,切点为E,且
上一点M,作圆C的一条切线ME,切点为E,且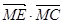 的最小值为4,求此抛物线准线的方程.
的最小值为4,求此抛物线准线的方程.
已知函数 (常数
(常数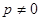 )在
)在 处取得极大值M=0.
处取得极大值M=0.
(Ⅰ)求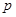 的值;
的值;
(Ⅱ)当 ,方程
,方程 有解,求
有解,求 的取值范围.
的取值范围.
如图:在多面体EF-ABCD中,四边形ABCD是平行四边形,△EAD为正三角形,且平面EAD 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
(Ⅰ)求证:BF AD;
AD;
(Ⅱ)求直线BD与平面BCF所成角的大小.
观察下列三角形数表
记第 行的第m个数为
行的第m个数为
 .
.
(Ⅰ)分别写出
 ,
,
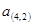 ,
,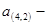
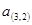 值的大小;
值的大小;
(Ⅱ)归纳出
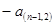 的关系式,并求出
的关系式,并求出 关于n的函数表达式.
关于n的函数表达式.
在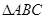 中,
中, 分别是角A、B、C的对边,且满足:
分别是角A、B、C的对边,且满足: .
.
(I)求C;
(II)当 时,求函数
时,求函数 的值域.
的值域.