如图,在四棱锥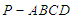 中,底面
中,底面 为菱形,
为菱形,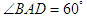 ,
,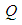 为
为 的中点。
的中点。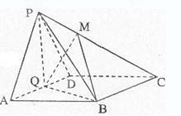
(1)若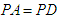 ,求证:平面
,求证:平面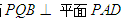 ;
;
(2)点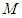 在线段
在线段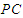 上,
上,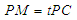 ,试确定
,试确定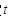 的值,使
的值,使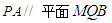 ;
;
(本题12分)某汽车厂有一条价值为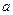 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值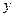 万元与技术改造投入
万元与技术改造投入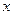 万元之间满足:①
万元之间满足:①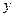 与
与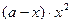 成正比;②当
成正比;②当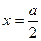 时,
时,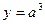 ,并且技术改造投入满足
,并且技术改造投入满足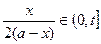 ,其中
,其中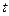 为常数且
为常数且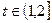 。
。
(1)求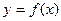 表达式及定义域;
表达式及定义域;
(2)求出产品增加值的最大值及相应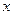 的值。
的值。
(本题12分)函数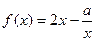 的定义域为
的定义域为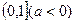 ,
,
(1)若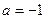 ,求函数
,求函数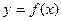 的值域;
的值域;
(2)求函数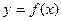 在
在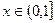 上的最大值和最小值,并求出函数取最值时相应
上的最大值和最小值,并求出函数取最值时相应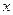 的值。
的值。
(本题12分)已知数列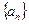 的前
的前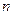 项和
项和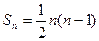 ,且
,且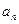 是
是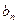 和1的等差中项。
和1的等差中项。
(1)求数列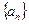 与
与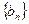 的通项公式;
的通项公式;
(2)若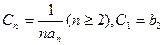 ,求
,求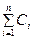 ;
;
(3)若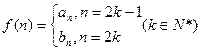 是否存在
是否存在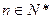 ,使
,使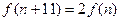 ?说明理由。
?说明理由。
(本题12分)已知命题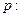 关于
关于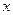 的方程
的方程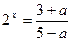 有负根;命题
有负根;命题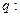 不等式
不等式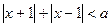 的解集为
的解集为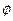 ,若
,若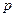 或
或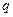 是真命题,
是真命题,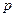 且
且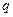 是假命题,求实数
是假命题,求实数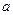 的范围。
的范围。
(本小题12分)
已知 ,
,
(1)判断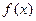 的奇偶性并用定义证明;
的奇偶性并用定义证明;
(2)当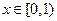 时,总有
时,总有 成立,求
成立,求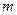 的取值范围.
的取值范围.