(本题12分)某汽车厂有一条价值为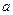 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值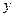 万元与技术改造投入
万元与技术改造投入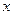 万元之间满足:①
万元之间满足:①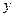 与
与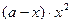 成正比;②当
成正比;②当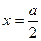 时,
时,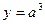 ,并且技术改造投入满足
,并且技术改造投入满足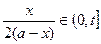 ,其中
,其中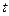 为常数且
为常数且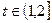 。
。
(1)求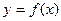 表达式及定义域;
表达式及定义域;
(2)求出产品增加值的最大值及相应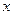 的值。
的值。
已知函数 在
在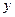 轴上的截距为1,且曲线上一点
轴上的截距为1,且曲线上一点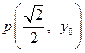 处的切线斜率为
处的切线斜率为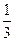 .(1)曲线在P点处的切线方程;(2)求函数
.(1)曲线在P点处的切线方程;(2)求函数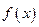 的极大值和极小值
的极大值和极小值
(本题14分)
已知函数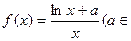 R).
R).
(1)若曲线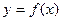 在点
在点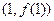 处的切线与直线
处的切线与直线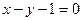 平行,求
平行,求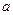 的值;
的值;
(2)在(1)条件下,求函数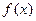 的单调区间和极值;
的单调区间和极值;
(3)当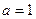 ,且
,且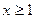 时,证明:
时,证明: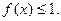
(本题13分)
已知数列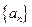 和
和 满足:
满足: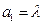 ,
,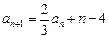 ,
, 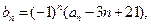 其中
其中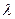 为实数,
为实数,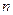 为正整数.
为正整数.
(Ⅰ)对任意实数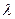 ,证明数列
,证明数列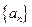 不是等比数列;
不是等比数列;
(Ⅱ)试判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(本题12分)
某民营企业生产A、B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图一所示;B产品的利润与投资的算术平方根成正比,其关系如图二所示(利润与投资单位:万元).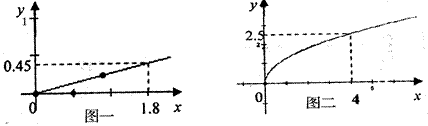
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
(本题12分)
研究问题:“已知关于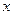 的不等式
的不等式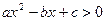 的解集为
的解集为 ,解关于
,解关于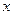 的不等式
的不等式 ”,有如下解法:
”,有如下解法:
解:由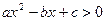
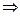
 ,令
,令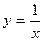 ,则
,则 ,
,
所以不等式 的解集为
的解集为 .
.
参考上述解法,已知关于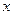 的不等式
的不等式 的解集为
的解集为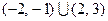 ,求关于
,求关于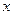 的不等式
的不等式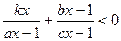 的解集.
的解集.