(14分) 点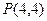 ,圆
,圆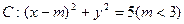 与椭圆
与椭圆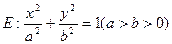 有一个公共点
有一个公共点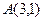 ,
,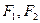 分别是椭圆的左右焦点,直线
分别是椭圆的左右焦点,直线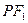 与圆
与圆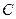 相切.
相切.
(1)求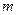 的值;(2)求椭圆
的值;(2)求椭圆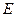 的方程。
的方程。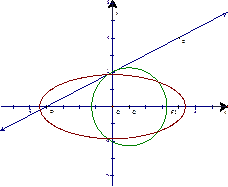
(本小题满分9分)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD= .
.
(1)求四棱锥S-ABCD的体积.
(2)求证:面SAB⊥面SBC.
(3)求SC与底面ABCD所成角的正切值.
(本小题满分9分)
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
(1)求证AC⊥BC1
(2)求证AC1∥平面CDB1
(本小题满分8分)
已知函数f(x)=|x+1|+ax,(a∈R)
(1)若a=1,画出此时函数的图象.
|
(2)若a>1,试判断函数f(x)在R上是否具有单调性.
(本小题满分8分)
设A ={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
(本小题满分8分)
已知三角形ABC的顶点坐标为A(0,3)、B(-2,-1)、C(4,3),M是BC边上的中点.
(1)求AB边所在的直线方程.
(2)求中线AM的长.
(3)求点C关于直线AB对称点的坐标.