如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并说明你的理由;
(2)若AB=,BC=2,求⊙O的半径.
某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周
(按 个工时计算)生产空调器、彩电、冰箱共
个工时计算)生产空调器、彩电、冰箱共 台,且冰箱至少生产
台,且冰箱至少生产 台,已知生
台,已知生
产这些家电产品每台所需工时和每台产值如下表
| 家电名称 |
空调 |
彩电 |
冰箱 |
| 工时 |
 |
 |
 |
| 产值(千元) |
 |
 |
 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少(以千元为单位)?
如图,开口向下的抛物线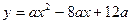 与
与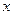 轴交于
轴交于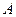 、
、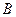 两点,
两点,
抛物线上另有一点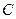 在第一象限,且使
在第一象限,且使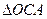 ∽
∽ ,(1)求
,(1)求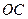 的长及
的长及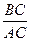 的值;(2)
的值;(2)
设直线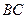 与
与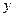 轴交于
轴交于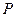 点,点
点,点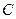 是
是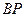 的中点时,求直线
的中点时,求直线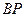 和抛物线的解析式。
和抛物线的解析式。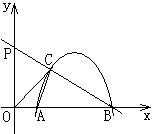
设 是不小于
是不小于 的实数,关于
的实数,关于 的方程
的方程
有两个不相等的实数根 、
、 ,
,
(1)若
 ,求
,求
 r 值;(2)求
r 值;(2)求 的最大值。
的最大值。
如图1,在第一象限内,直线y=mx与过点B(0,1)且平行于x轴的直线l相交于点A,半径为r的⊙Q与直线y=mx、x轴分别相切于点T、E,且与直线l分别交于不同的M、N两点.
(1)当点A的坐标为( ,p)时,
,p)时,
①填空:p=___,m= ___,∠AOE= ___.
②如图2,连接QT、QE,QE交MN于点F,当r=2时,试说明:以T、M、E、N为顶点的四边形是等腰梯形;
(2)在图1中,连接EQ并延长交⊙Q于点D,试探索:对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值会变化吗?若不变,求出a的值;若变化.请说明理由.
如图,在直角坐标系中,点A的坐标为(0,8),点B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.
(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.