(本小题满分12分)
已知椭圆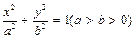 的左、右焦点分别为
的左、右焦点分别为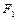 、
、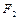 ,离心率
,离心率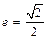 ,右准线方程为
,右准线方程为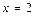 .
.
(I)求椭圆的标准方程;
(II)过点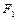 的直线
的直线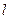 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且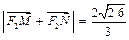 ,求直线
,求直线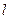 的方程.
的方程.
已知函数 .(I)当
.(I)当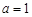 时,求函数
时,求函数 的单调区间;(II)若函数
的单调区间;(II)若函数 的图象在点
的图象在点 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
已知椭圆 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点 的最短距离为
的最短距离为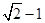 .(Ⅰ)求椭圆C的方程;(Ⅱ)过点
.(Ⅰ)求椭圆C的方程;(Ⅱ)过点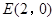 且斜率为
且斜率为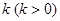 的直线
的直线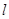 与
与 交于
交于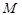 、
、 两点,
两点,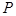 是点
是点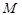 关于
关于 轴的对称点,证明:
轴的对称点,证明: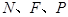 三点共线.
三点共线.
如图,多面体ABCDS中,面ABCD为矩形,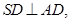 且
且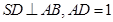 ,
,
 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。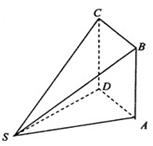
对某校高三年级学生参加社区服务次数进行统计, 随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: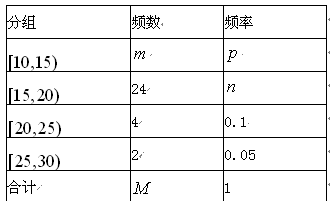
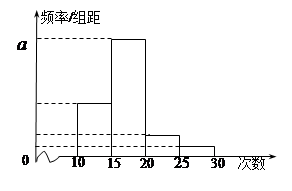
(Ⅰ)求出表中 、
、 及图中
及图中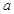 的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间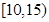 内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间 内的概率.
内的概率.
(满分12分)过点 的且斜率为
的且斜率为 直线
直线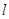 与
与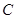 为圆心的圆
为圆心的圆 交于A、B两点,O为原点,M是AB中点。
交于A、B两点,O为原点,M是AB中点。
(1)若 ,求
,求 值;
值;
(2)若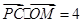 ,求直线
,求直线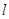 的方程。[来
的方程。[来